算法中使用哨兵变量(TODO)
背景
哨兵,现实中是用于解决国家之间的边界问题。
在算法程序中,我们设置一些冗余的变量,让算法程序处理边界问题时更加容易,这些变量就被称为哨兵。
本文将会举例说明,哨兵变量在算法程序中的应用。
插入排序
插入排序是一种常用的排序算法,它的思路是
- 用 i 从 1 开始遍历数组中每个元素
- 从后往前遍历 1-i 的每个元素,找到第一个比当前元素小的元素,将其插入到该元素之后
- Note: 先挪位置,循环结束后再在 j 指示的索引中(第一个比当前元素小的元素)插入当前值
func InsertSort[T ttypes.Number](arr []T) []T {
res := make([]T, len(arr))
copy(res, arr)
for i := 1; i < len(res); i++ {
j := i
current := res[i]
for j > 0 && res[j-1] > current {
res[j] = res[j-1]
j--
}
res[j] = current
}
return res
}
演示图:
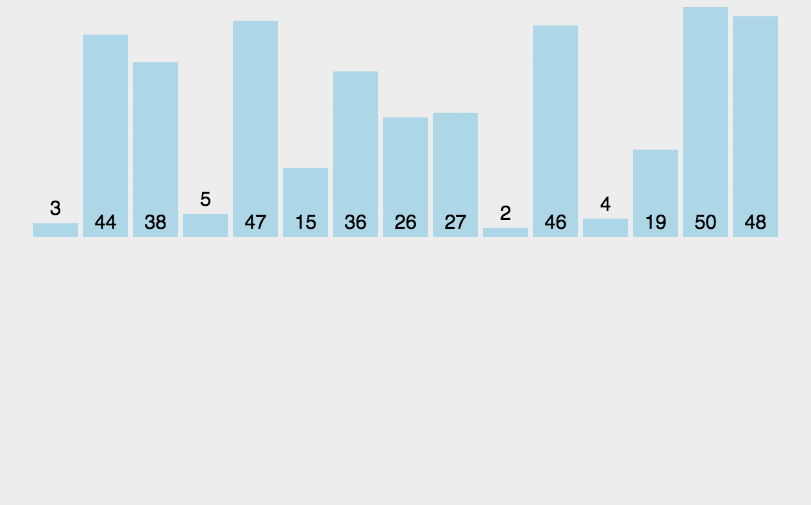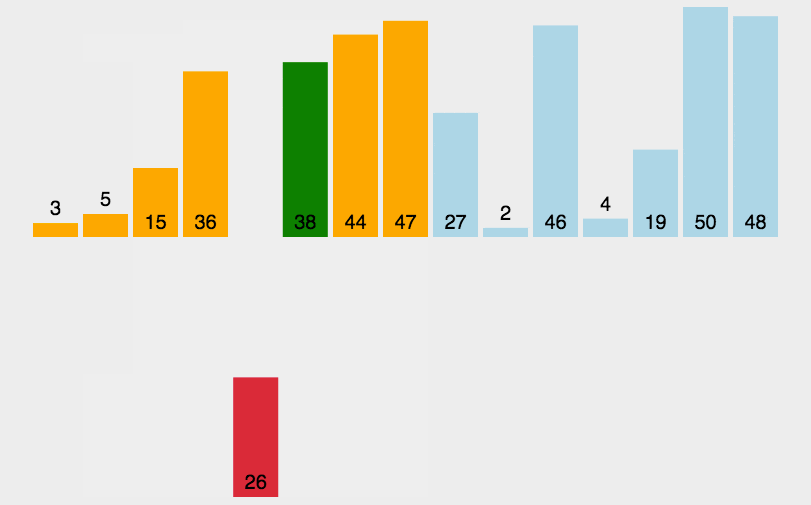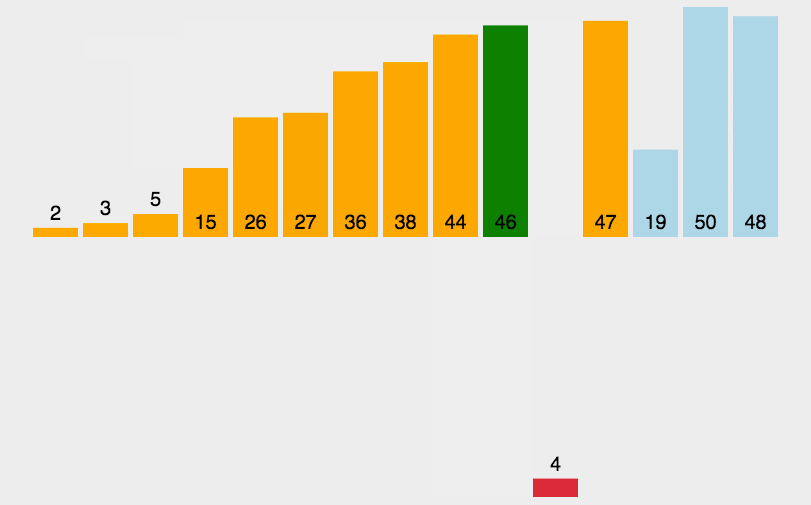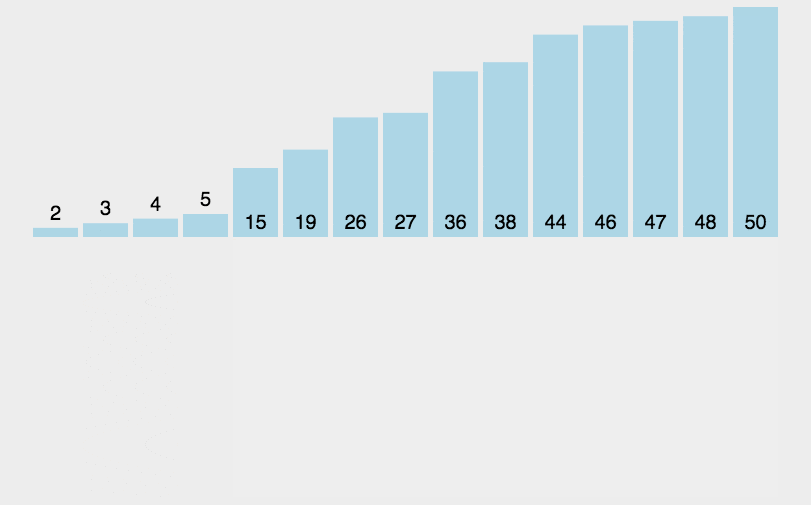
哨兵模式
哨兵模式的代码如下,它在数组的前面添加一个元素。
每次开始遍历前,它将当前需要插入的元素放到数组头部(res[0])。这样就算 1-i 中没有比 res[i] 小的元素,但循环到最后还是会触发条件 not (res[0] > current), 达到跳出循环的目的。
在哨兵模式的插入排序中,我们利用一个元素的内存,省去 j>0 这个判断条件。
func InsertSortWithSentinel[T ttypes.Number](arr []T) []T {
res := make([]T, len(arr))
copy(res, arr)
res = append([]T{0}, res...)
for i := 2; i < len(res); i++ {
j := i
current := res[i]
res[0] = current
// 和无哨兵相比,省略掉了 j > 0 这个比较条件
for res[j-1] > current {
res[j] = res[j-1]
j--
}
res[j] = current
}
return res[1:]
}
链表
链表节点的定义如下
//SingleListNode 单链表
type SingleListNode[T any] struct {
Data T
Next *SingleListNode[T]
}
Append
Append 函数用于向链表的尾部添加节点,下面的程序分别是普通写法和添加了哨兵节点的写法
- 普通写法
func Append[T any](head *SingleListNode[T], val T) *SingleListNode[T] {
var node = &SingleListNode[T]{
Next: nil,
Data: val,
}
if head == nil {
return node
}
var current = head
for current.Next != nil {
current = current.Next
}
current.Next = node
return head
}
- 添加了哨兵节点的写法
func AppendDummy[T any](head *SingleListNode[T], val T) *SingleListNode[T] {
var node = &SingleListNode[T]{
Next: nil,
Data: val,
}
var dummy = &SingleListNode[T]{
Next: head,
}
var current = dummy
for current.Next != nil {
current = current.Next
}
current.Next = node
return dummy.Next
}
在普通写法中,需要先判断 if head == nil,避免 for 循环中 current.Next 出错。
在哨兵节点写法中,我们在链表的头节点之前加了一个 dummy 节点,这样 current.Next 就一定不会是空了,因此可以省略掉 if 判断语句。
DeleteVal
DeleteVal 函数用于从链表中删除指定值的节点,以下是它的两种写法:
- 普通写法
func DeleteVal[T string](head *SingleListNode[T], val T) *SingleListNode[T] {
if head == nil {
return head
}
if head.Data == val {
return head.Next
}
var current = head
for current.Next != nil {
if current.Next.Data == val {
current.Next = current.Next.Next
break
}
current = current.Next
}
return head
}
- 哨兵节点写法
func DeleteValDummy[T string](head *SingleListNode[T], val T) *SingleListNode[T] {
var dummy = &SingleListNode[T]{
Next: head,
}
var current = dummy
for current.Next != nil {
if current.Next.Data == val {
current.Next = current.Next.Next
break
}
current = current.Next
}
return dummy.Next
}
在 DeleteVal 中,我们需要先判断 head 是否为空,head 是否就是要查找的节点。然后才能开始循环,挨个判断 current.Next 是否是查找的节点。
在 DeleteValDummy 中,我们在头节点之前添加了一个哨兵节点 Dummy。
- 这样第一个节点肯定不会是空,
if head == nil可以省略 - 判断的第一个节点是
Dummy.Next即head,if head.Data == val也省略。
返回所有二叉搜索树
题目
给你一个整数 n ,请你生成并返回所有由 n 个节点组成且节点值从 1 到 n 互不相同的不同二叉搜索树 。可以按 任意顺序 返回答案。
不缓存结果的动态规划解法
这个问题我们可以用动态规划的思路来解题。
递推公式:
令:
- \( f(1, n) \) 表示 1-n 组成的互补相同的二叉搜索树的集合。
上述公式表示,从 1 到 n, 分别以每个数作为根节点,利用剩下的数组成两个二叉搜索树,最终计算出来 1-n 的二叉搜索树的集合。
上述公式,将大问题 \( f(1, n) \) 分解成了小问题 \( f(1, i-1), f(i+1, n) \)
递归出口:
当 \( f(i, j) \) 中,i > j 的时候,即此时计算的子树是 0 个节点,那么 \( f(i, j) \) 返回一个空数组。
普通解法的代码
func genTreeTedious(start, end int) []*lt.TreeNode {
var res = make([]*lt.TreeNode, 0)
for root := start; root <= end; root++ {
leftTrees := genTreeTedious(start, root-1)
rightTrees := genTreeTedious(root+1, end)
if len(leftTrees) == 0 && len(rightTrees) == 0 {
tree := <.TreeNode{
Val: root,
Left: nil,
Right: nil,
}
res = append(res, tree)
} else if len(leftTrees) == 0 {
for _, right := range rightTrees {
tree := <.TreeNode{
Val: root,
Left: nil,
Right: right,
}
res = append(res, tree)
}
} else if len(rightTrees) == 0 {
for _, left := range leftTrees {
tree := <.TreeNode{
Val: root,
Left: left,
Right: nil,
}
res = append(res, tree)
}
} else {
for _, left := range leftTrees {
for _, right := range rightTrees {
tree := <.TreeNode{
Val: root,
Left: left,
Right: right,
}
res = append(res, tree)
}
}
}
}
return res
}
在上述代码中,我们在递归出口中,直接返回了一个空数组,那么它的上一层就需要判断当前子树是否到了递归出口,如果是,则补充上一个叶子节点。
由于需要判断,左右子树同时达到出口,左子树达到出口,右子树达到出口三种情况,代码整体看起来很繁琐。
添加了哨兵之后的代码
func genTree(start, end int) []*lt.TreeNode {
var res = make([]*lt.TreeNode, 0)
// 这一句让, leftTrees 和 rightTrees 返回的长度不是0, 而是1, 里面的值是 nil
if start > end {
return []*lt.TreeNode{nil}
}
for root := start; root <= end; root++ {
leftTrees := genTree(start, root-1)
rightTrees := genTree(root+1, end)
for _, left := range leftTrees {
for _, right := range rightTrees {
tree := <.TreeNode{
Val: root,
Left: left,
Right: right,
}
res = append(res, tree)
}
}
}
return res
}
上述代码和前一小节的代码思路是一样的,不过在递归出口处,不是返回一个空数组,而是返回包含一个 nil 元素的数组。
这样递归出口的上一层,不需要判断下一层是否达到了出口,直接使用下一层返回的子树 nil 作为叶子节点的 Left 和 Right 的值。
这样使用了包含了 nil 的数组作为哨兵之后,代码整体看起来简洁了很多。