变态跳台阶问题的解题思路

简介：本文主要记录了 变态跳台阶问题 的推导过程

题目描述

一只青蛙一次可以跳上1级台阶，也可以跳上2级……它也可以跳上n级。求该青蛙跳上一个n级的台阶总共有多少种跳法。

解题思路

问题转换

这个问题我们可以转换思路，将其转换成求树的节点0的个数的题目。

假设存在一棵树，它的根节点是N，它的子节点从左往右依次为 n-1, n-2, … 直到0。

同理，根节点子节点的子节点也遵循这样的规律，0节点没有子节点。请问在这棵树中，0节点一共有多少个？

根节点为3的树如下图所示:

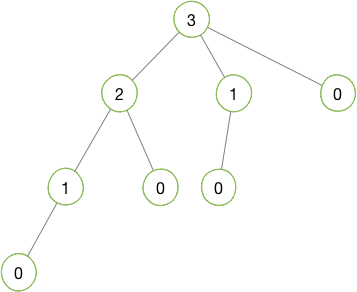
从 0 到 3 的路径可以认为是青蛙跳到三阶台阶上的路径，0 的个数就是跳法的个数

答案推导

如上所示，我们已经将问题转换成了求树中0节点的个数，根据树的递归定义，我们可以得到如下的定义:

• \(f(1) = 1\)
• \(f(n) = f(n-1) + f(n-2) + … + f(1) + 1\)
• \(f(n-1) = \space \space \space \space \space \space \space \space \space \space \space \space f(n-2) + … + f(1) + 1\)

令\(f(n) - f(n-1)\)，可得：\(f(n) = 2 * f(n-1)\)。

根据\(f(1) = 1\)和\(f(n) = 2 * f(n-1)\)，我们最终可以得到，\(f(n) = 2^{n-1}\)。

最终答案

有了上面的推导过程，最终的编程实现很简单，我们只需要返回\(2^{n-1}\)即可，答案如下:

#include <cmath>

class Solution {
public:
    int jumpFloorII(int number) {
        return pow(2, number - 1);
    }
};