Leetcode第96题

题目

给你一个整数 n ，求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种？返回满足题意的二叉搜索树的种数。

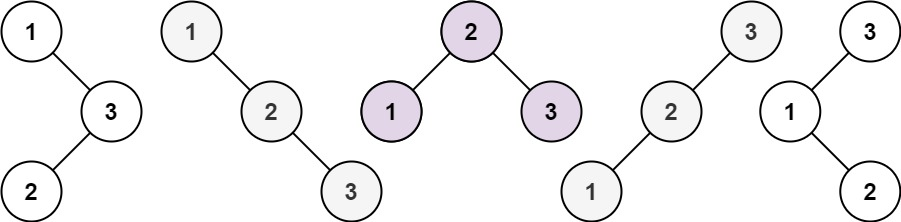
示例 1：

输入：n = 3 输出：5

示例 2：

输入：n = 1 输出：1

提示：

1 <= n <= 19

解题思路

这个题目主要的难度在公式推导上，我们可以用动态规划的思路来求解。

• 令 \( G(N) \) 表示 n 互不相同的整数组成的二叉搜索树的数量。
• \( F(i, N) \) 表示由 i 作为根节点，N 个互补相同的整数组成的二叉搜索树的数量
• 可得, \( G(N) \) 是由每个 i 作为根节点的互不相同的二叉搜索树的数量的总和，此公式记做公式(1)

接着，我们需要再推导出 \( F(i, N) \) 和 \( G(N) \) 的关系，就可以得到我们的递推公式了。

要想求 i 作为根节点，N 个互补相同的整数组成的二叉搜索树的数量，我们可以先求出左右两个子树的数量，左右两个子树相乘，即是总的数量。

例如，对于 1-7 组成, 3 作为根节点的二叉搜索树，左子树是 1-2 组成的二叉搜索树，右子树是 4-7 组成的二叉搜索树。

又由于 5-7 和 1-3 都是三个节点，它们组成的二叉搜索树虽然值不同，但是树的数量是相同的。可得

进一步推广，我们可以得到公式(2)

结合公式1和公式2, 我们可以得到递推公式

递推出口，也非常容易得到，树是0个或1个节点的时候，它的数量都是 1, 即

题目要求的 由 n 个节点组成且节点值从 1 到 n 互不相同的二叉搜索树的数量 即是 \( G(N) \)

代码及复杂度

有了递推公式和递推出口之后，代码编写起来就非常容易了

func numTrees(n int) int {
	G := make([]int, n+1)
	G[0] = 1
	G[1] = 1
	for N := 2; N <= n; N++ {
		for i := 1; i <= N; i++ {
			G[N] += G[i-1] * G[N-i]
		}
	}

	return G[n]
}

上述代码的复杂度也非常容易分析

• N 表示输入的整数
• 时间复杂度 是看循环执行的次数，这是一个等差数列，所以时间复杂度是 \( O(N^2) \)
• 空间复杂度 是看 G 数组的长度, 空间复杂度是 \( O(N) \)